This week, Mohamed Mekkouri from Hugging Face published a blog post to share their success in fine-tuning LLMs to 1.58bit. This announcement motivated me to share my by-hand exercise for BitNets.
Some may remember last October researchers at Microsoft published an article about BitNet. It generated a ton of interests. I sketched an exercise. But I didn't post it.
I was skeptical about whether or not BitNet would be practical for real-world use, because training a BitNet still needs to run pre-training from scratch, and very few has the resources to do it.
Therefore, when I read HF's successful attempt to fine-tune a BitNet using only 10B tokens to achieve performance comparable to that of Llama 2, I begin to see the promise of BitNets.
BitNets deserve a spot to be the No. 29 in the AI by Hand ✍️ Advanced Series. I spent some time to clean up my sketch. Now I am ready to share this exercise with you. 🙌
In this exercise, I'd like to draw your attention to the following comparisons:
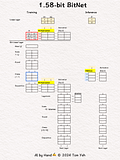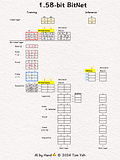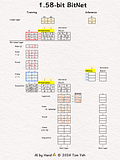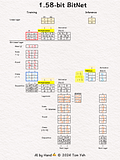
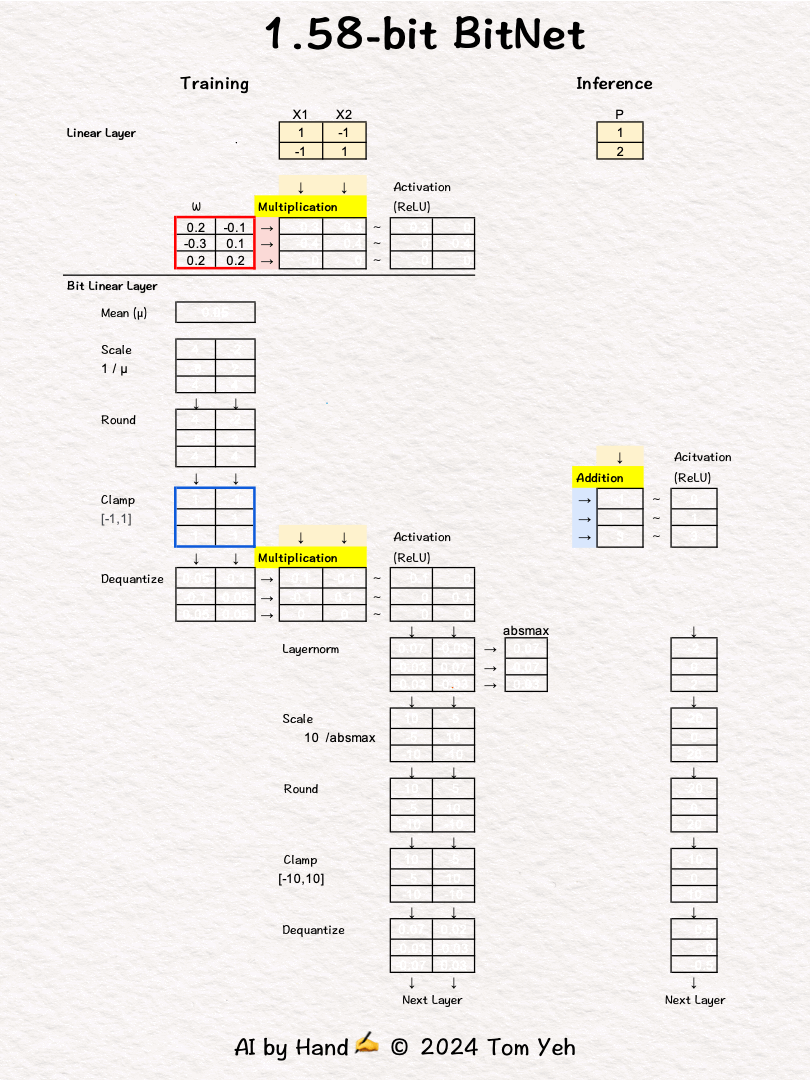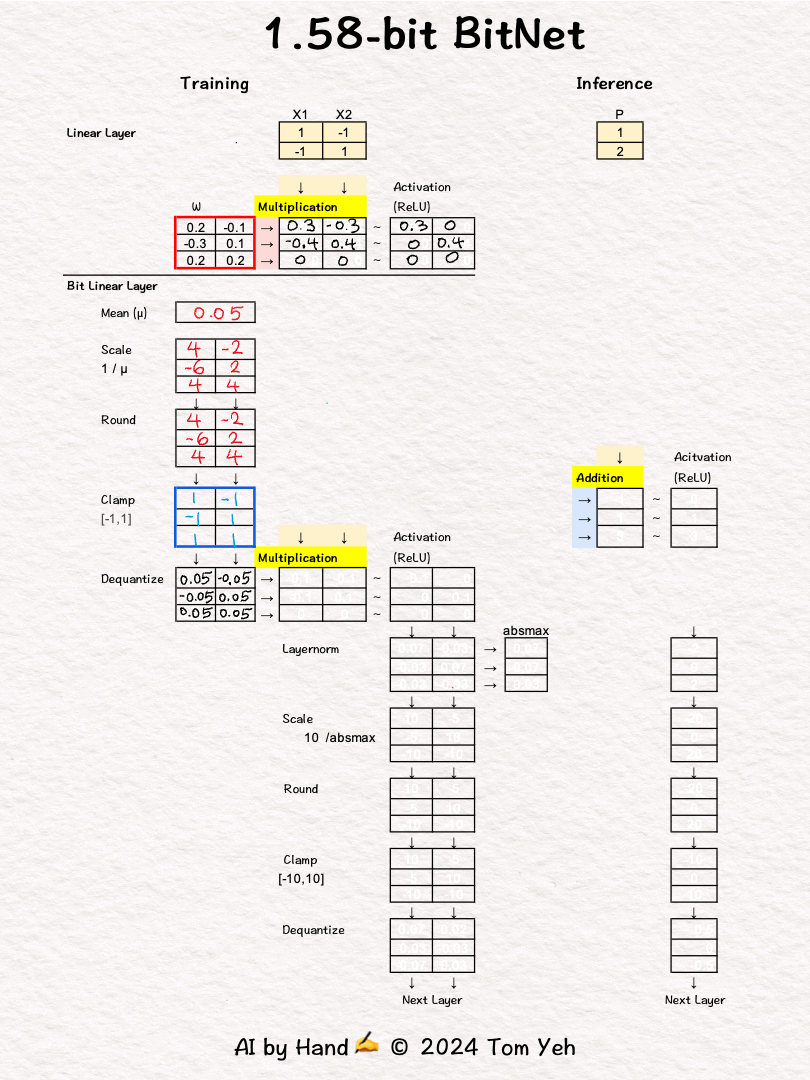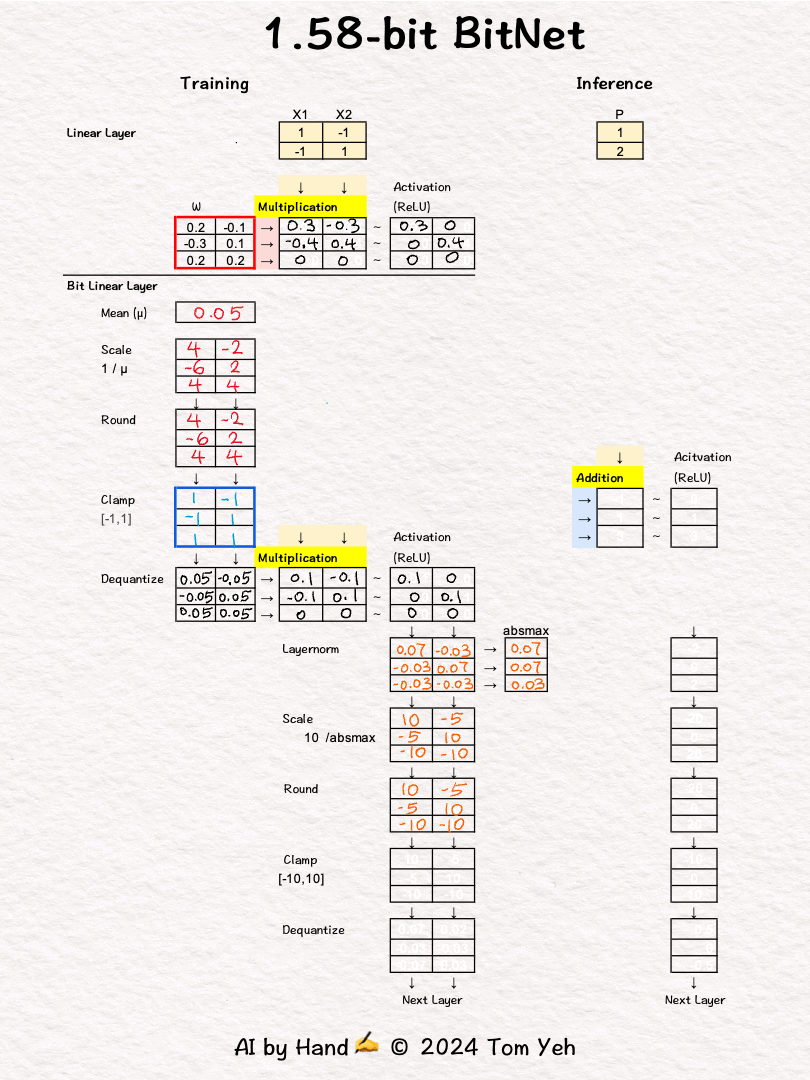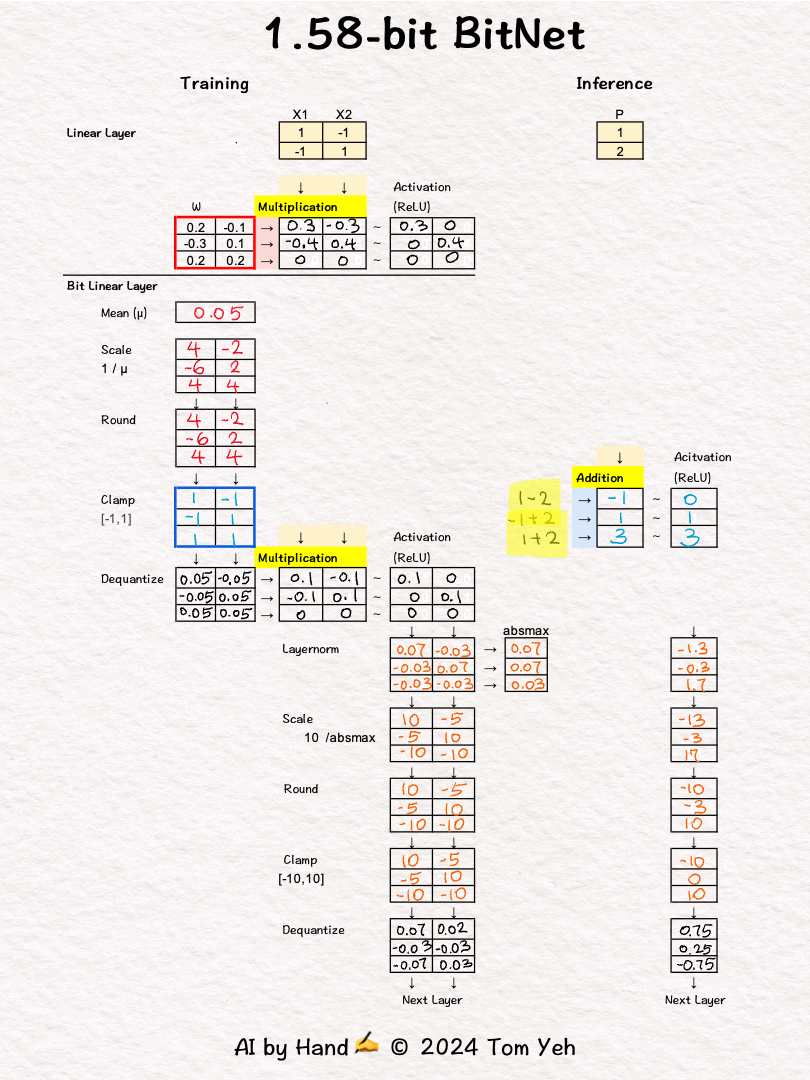
💡 Linear vs. Bit Linear
In a regular linear layer layer, no quantization.
In a bit linear layer, extreme quantization happens, to only three choices: [-1, 0, 1]. According to information theory, it takes 1.58 bits to encode three choices. That's why they call it 1.58bit BitNet.
💡 Training vs Inference
In training, full precision weights are used in forward and backward passes (red border 🟥) to run back propagation and gradient decent to update and refine weights
In inference, only the [-1,0,1] weights are used (blue border 🟦 ).
💡 Multiplication vs Addition
The multiplication operation in a regular linear layer is reduced to much simpler addition operation. I highlighted the the operations in yellow 🟨 to help you see the contrast easily.
I hope the rest is self-explanatory. If not, please ask questions in the comment!


Sorry, I cannot get how to calculate the mean at the beginning of the Bit linear layer.
can you do swin transformers by hand?