14. Vector Database
Can you calculate this by hand? ✍️
Vector databases are revolutionizing how we search and analyze complex data. They have become the backbone of Retrieval Augmented Generation (RAG).
How do vector databases work?
[1] Given
↳ A dataset of three sentences, each has 3 words (or tokens)
↳ In practice, a dataset may contain millions or billions of sentences. The max number of tokens may be tens of thousands (e.g., 32,768 mistral-7b).
Process "how are you"
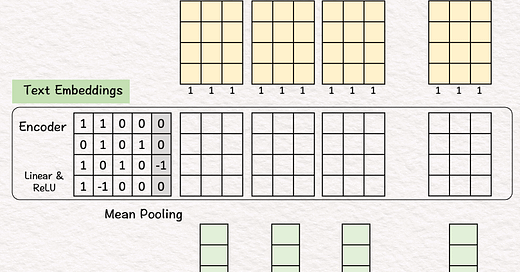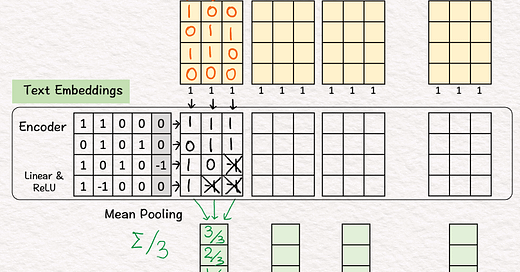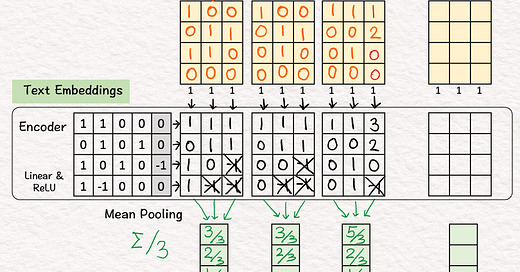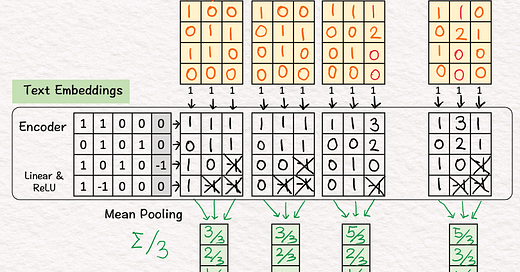
[2] 🟨 Word Embeddings
↳ For each word, look up corresponding word embedding vector from a table of 22 vectors, where 22 is the vocabulary size.
↳ In practice, the vocabulary size can be tens of thousands. The word embedding dimensions are in the thousands (e.g., 1024, 4096)
[3] 🟩 Encoding
↳ Feed the sequence of word embeddings to an encoder to obtain a sequence of feature vectors, one per word.
↳ Here, the encoder is a simple one layer perceptron (linear layer + ReLU)
↳ In practice, the encoder is a transformer or one of its many variants.
[4] 🟩 Mean Pooling
↳ Merge the sequence of feature vectors into a single vector using "mean pooling" which is to average across the columns.
↳ The result is a single vector. We often call it "text embeddings" or "sentence embeddings."
↳ Other pooling techniques are possible, such as CLS. But mean pooling is the most common.
[5] 🟦 Indexing
↳ Reduce the dimensions of the text embedding vector by a projection matrix. The reduction rate is 50% (4->2).
↳ In practice, the values in this projection matrix is much more random.
↳ The purpose is similar to that of hashing, which is to obtain a short representation to allow faster comparison and retrieval.
↳ The resulting dimension-reduced index vector is saved in the vector storage.
[6] Process "who are you"
↳ Repeat [2]-[5]
[7] Process "who am I"
↳ Repeat [2]-[5]
Now we have indexed our dataset in the vector database.
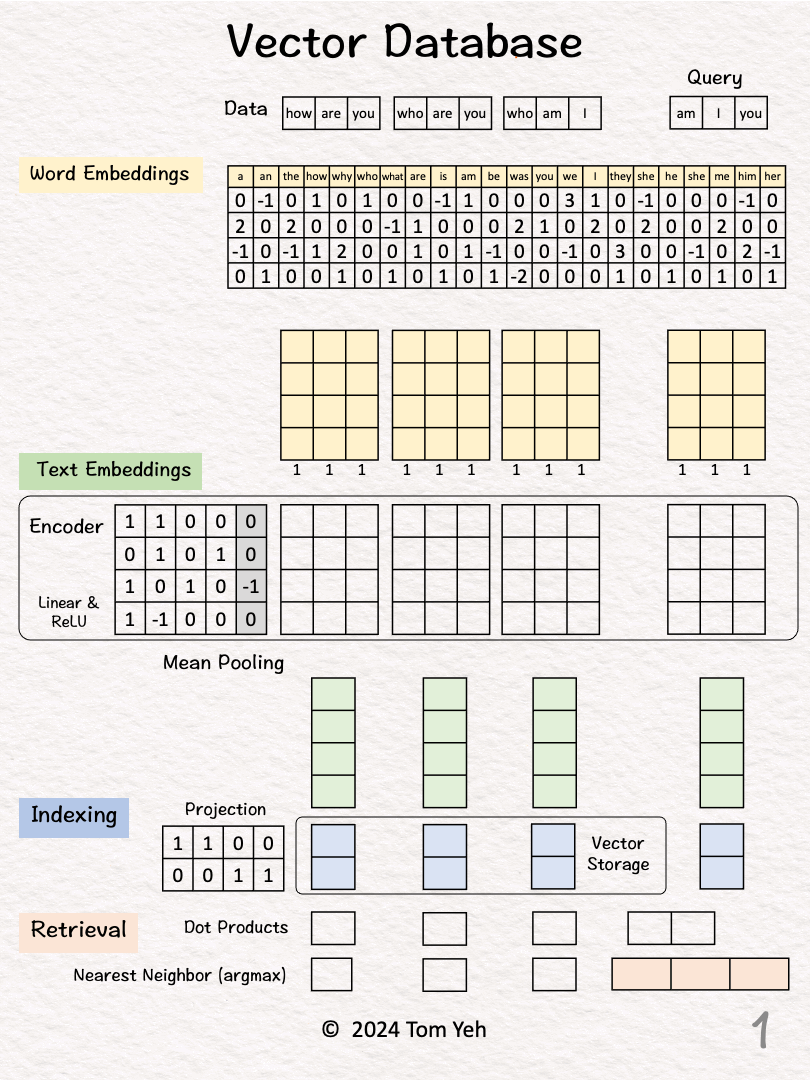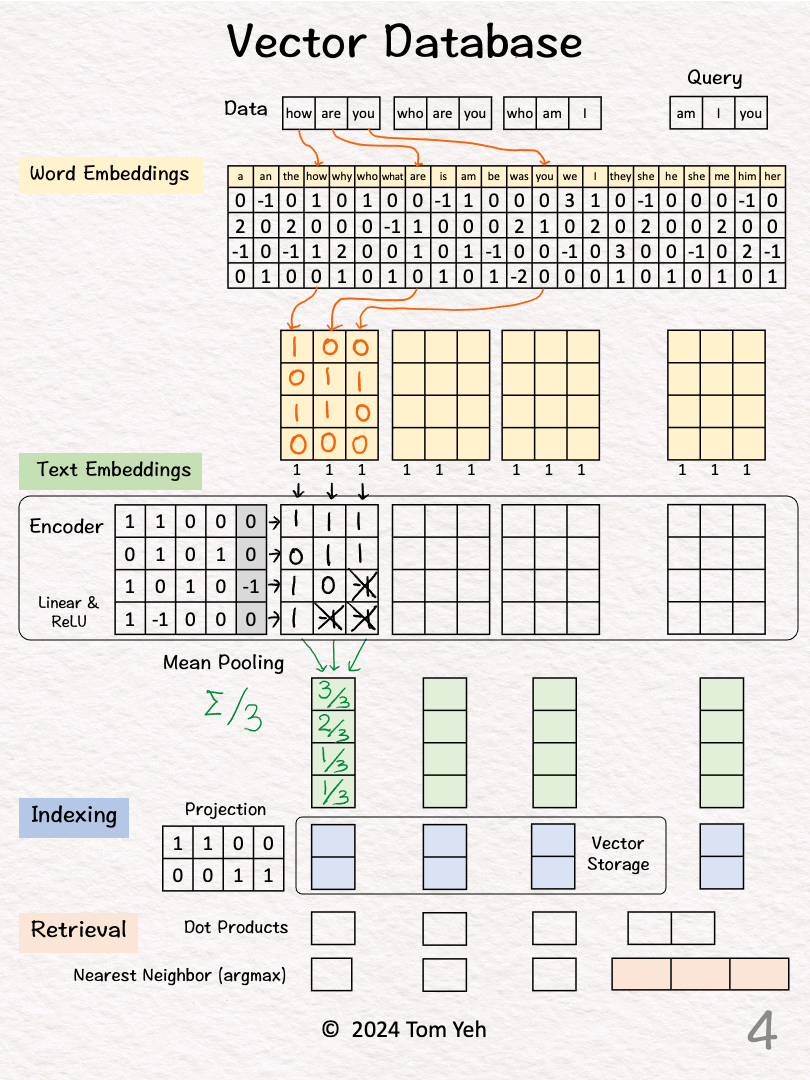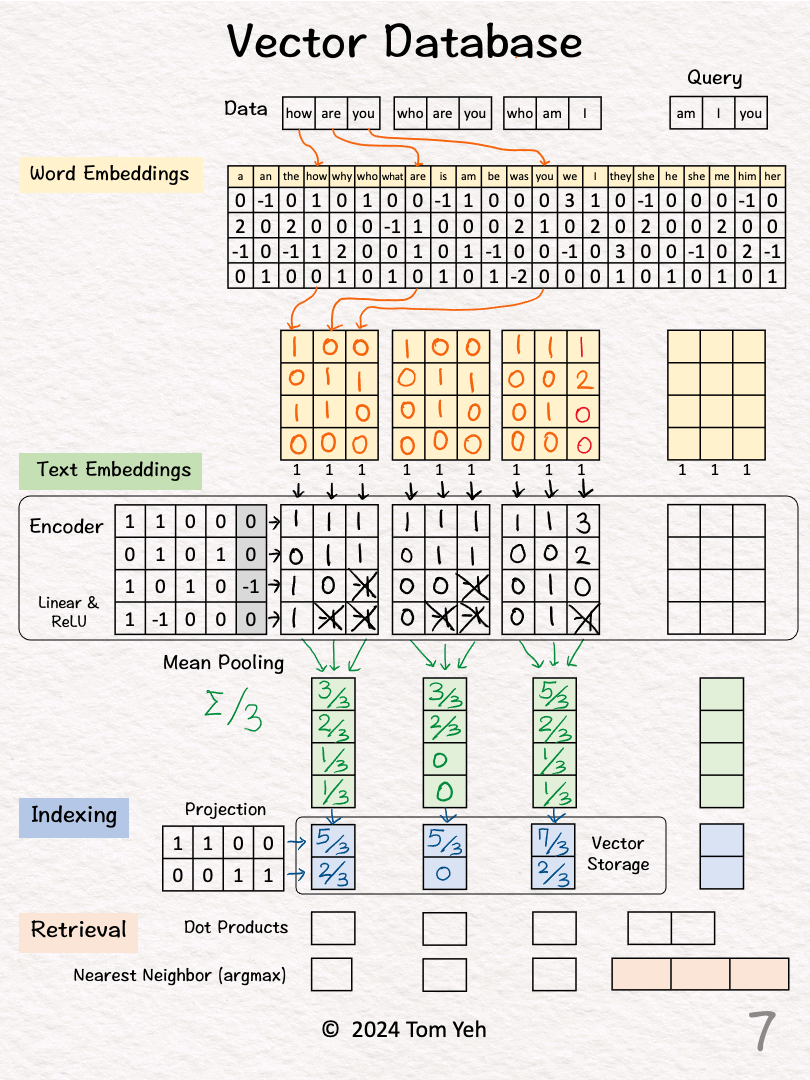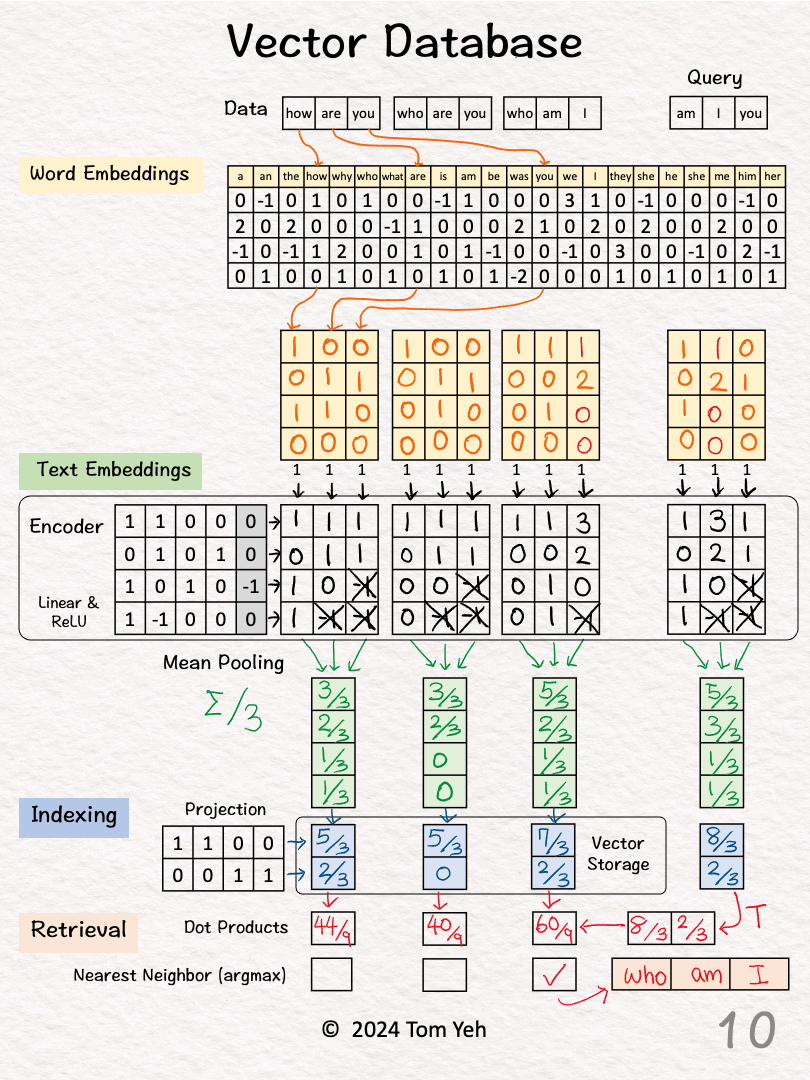
[8] 🟥 Query: "am I you"
↳ Repeat [2]-[5]
↳ The result is a 2-d query vector.
[9] 🟥 Dot Products
↳ Take dot product between the query vector and database vectors. They are all 2-d.
↳ The purpose is to use dot product to estimate similarity.
↳ By transposing the query vector, this step becomes a matrix multiplication.
[10] 🟥 Nearest Neighbor
↳ Find the largest dot product by linear scan.
↳ The sentence with the highest dot product is "who am I"
↳ In practice, because scanning billions of vectors is slow, we use an Approximate Nearest Neighbor (ANN) algorithm like the Hierarchical Navigable Small Worlds (HNSW).
