24. Variational Auto Encoder (VAE)

Can you calculate this by hand? ✍️

A Variational Auto Encoder (VAE) learns the structure (mean and variance) of hidden features and generates new data from the learned structure.

In contrast, GANs only learn to generate new data to fool a discriminator; they may not necessarily know the underlying structure of the data.

The International Conference on Learning Representations (ICLR) this year announced its first ever "Test of Time Award" to recognizes the VAE paper, published 10 years ago.

"𝘈𝘶𝘵𝘰-𝘌𝘯𝘤𝘰𝘥𝘪𝘯𝘨 𝘝𝘢𝘳𝘪𝘢𝘵𝘪𝘰𝘯𝘢𝘭 𝘉𝘢𝘺𝘦𝘴" by Diederik Kingma and Max Welling.

How does a VAE work?

Walkthrough

[1] Given:
↳ Three training examples X1, X2, X3
↳ Copy training examples to the bottom
↳ The purpose is to train the network to reconstruct the training examples.
↳ Since each target is a training example itself, we use the Greek word "auto" which means "self." This crucial step is what makes an autoencoder "auto."

[2] Encoder: Layer 1 + ReLU
↳ Multiply inputs with weights and biases
↳ Apply ReLU, crossing out negative values (-1 -> 0)

[3] Encoder: Mean and Variance
↳ Multiply features with two sets of weights and biases
↳ 🟩 The first set predicts the means (𝜇) of latent distributions
↳ 🟪 The second set predicts the standard deviation (𝜎) of latent distributions

[4] Reparameterization Trick: Random Offset
↳ Sample epsilon ε from the normal distribution with mean = 0 and variance = 1.
↳ The purpose is to randomly pick a offset away from the mean.
↳ Multiply the standard deviation values with epsilon values.
↳ The purpose is to scale the offset by the standard deviation.

[5] Reparameterization Trick: Mean + Offset
↳ Add the sampled offset to predicted mean
↳ The result are new parameters or features 🟨 as inputs to the Decoder.

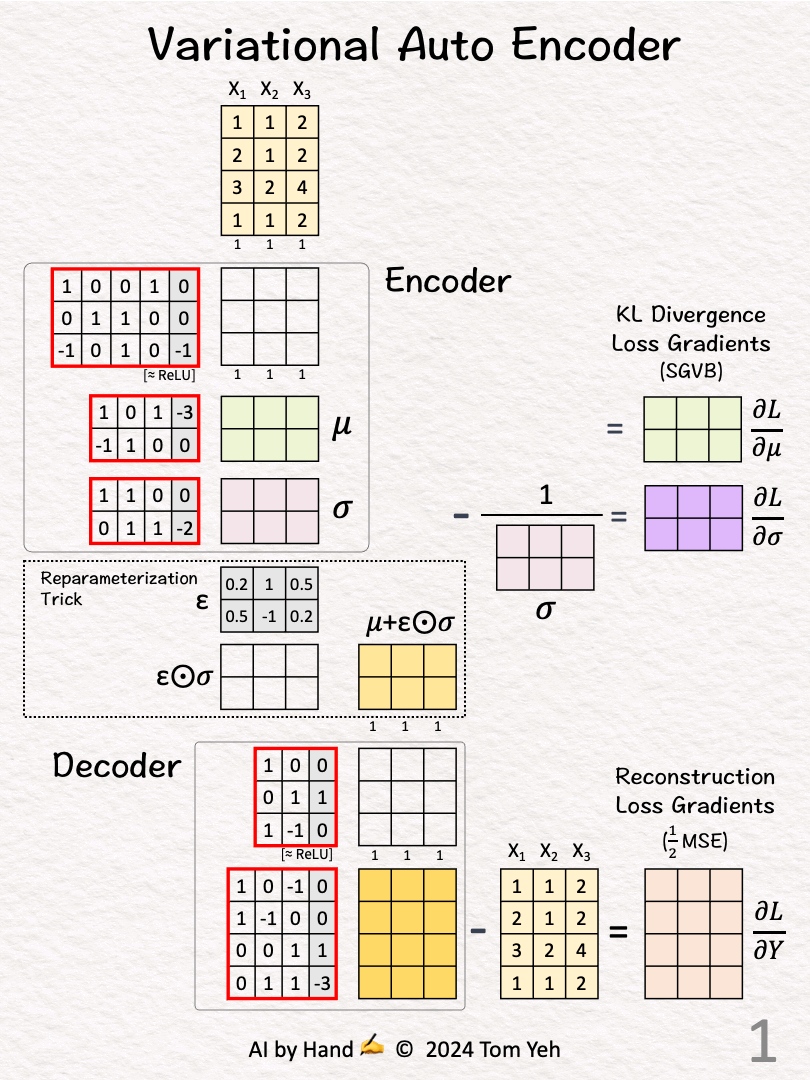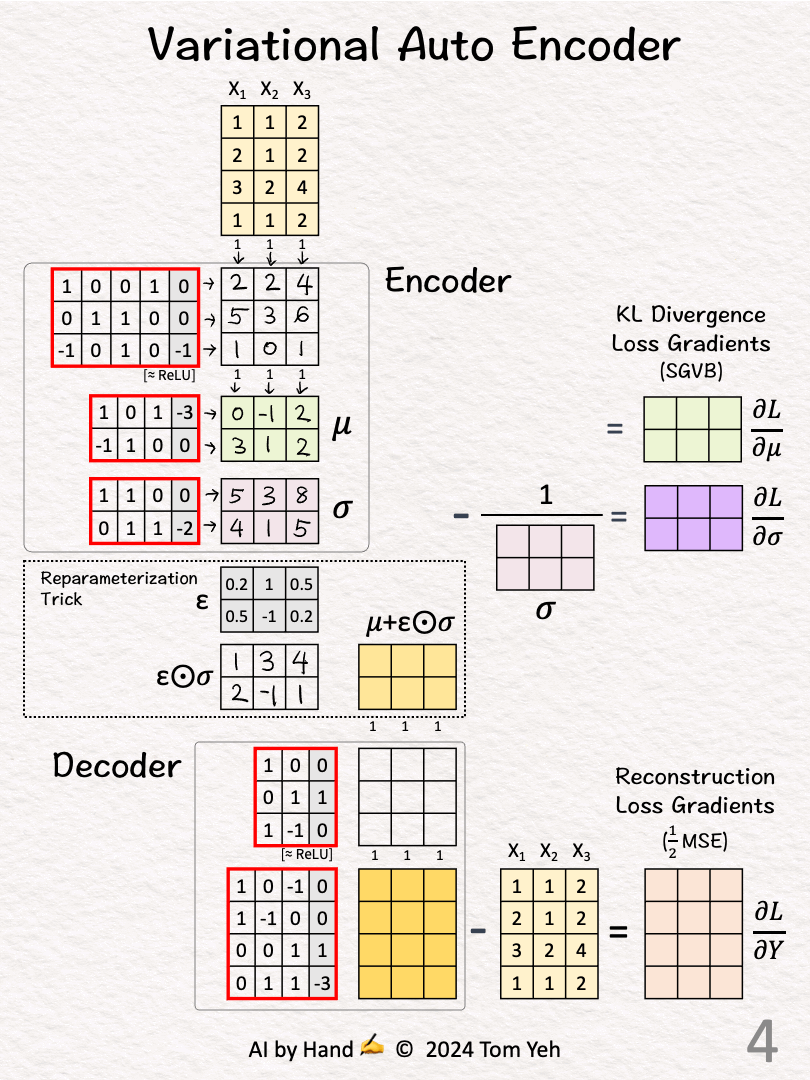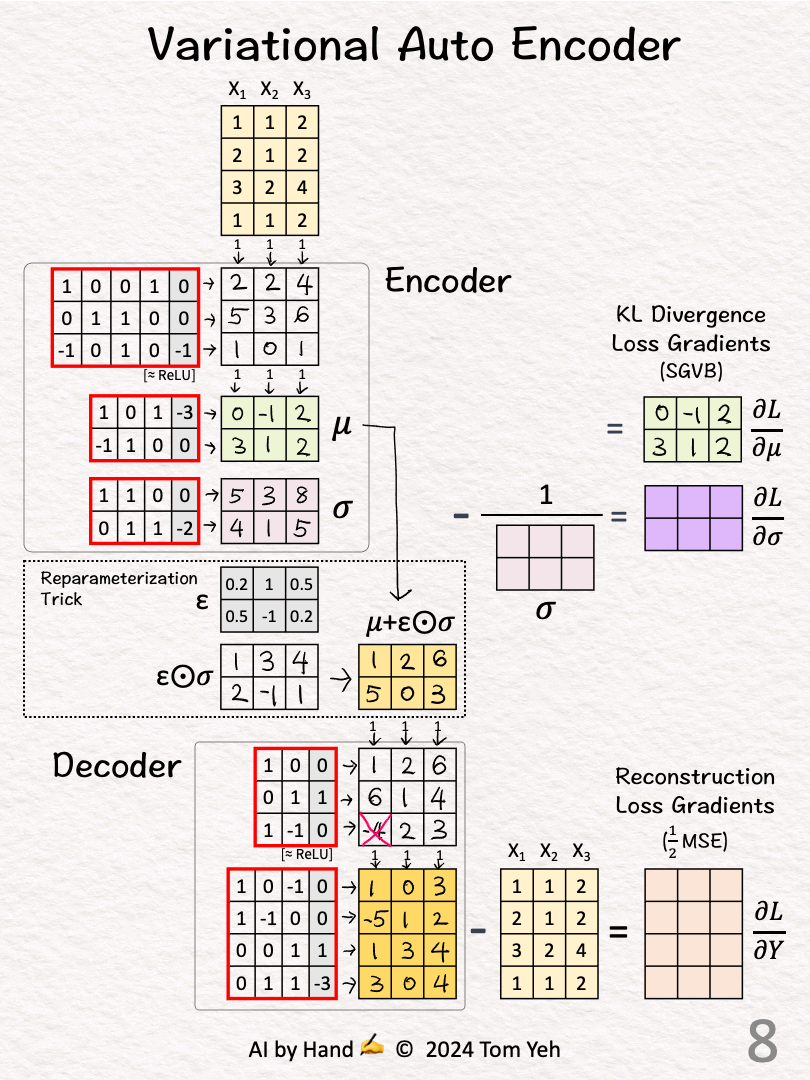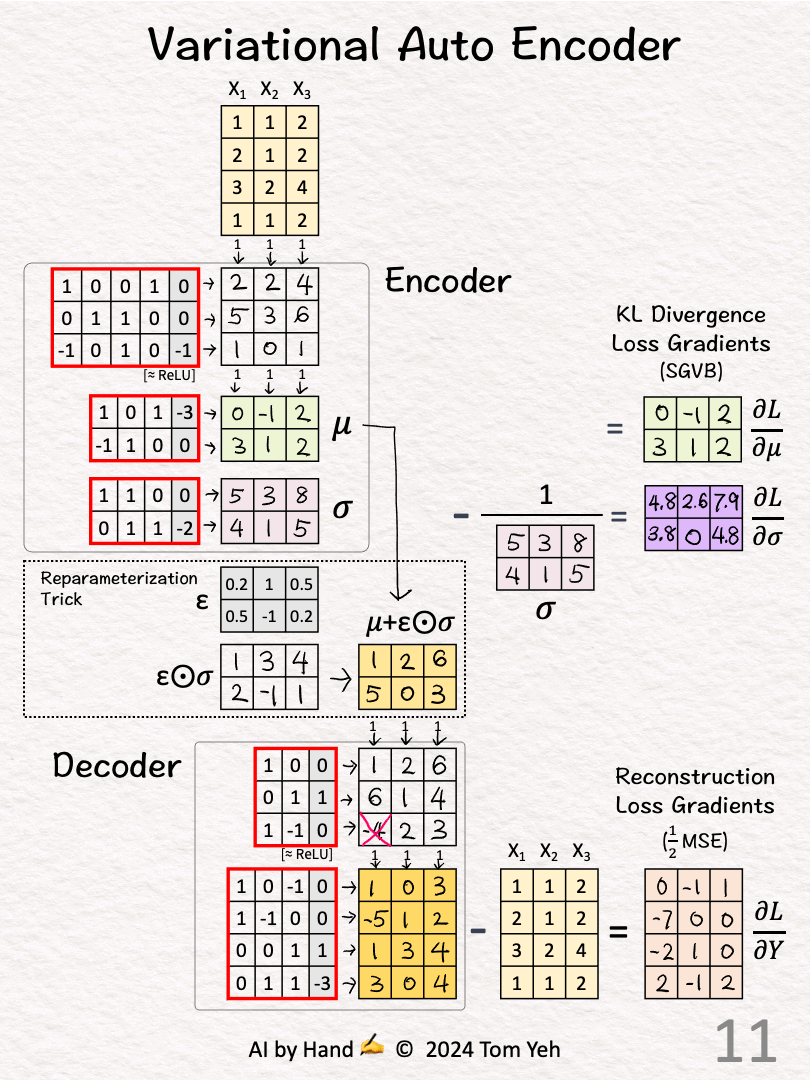
[6] Decoder: Layer 1 + ReLU
↳ Multiply input features with weights and biases
↳ Apply ReLU, crossing out negative values. Here, -4 is crossed out.

[7] Decoder: Layer 2
↳ Multiply features with weights and biases
↳ The output is Decoder's attempt to reconstruct the input data X from reparameterized distributions described by 𝜇 and 𝜎.

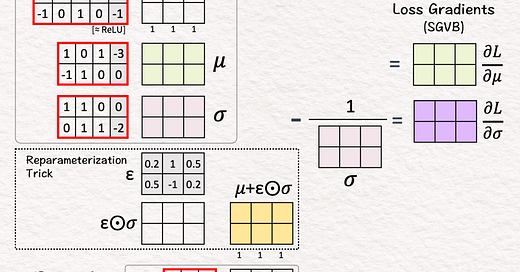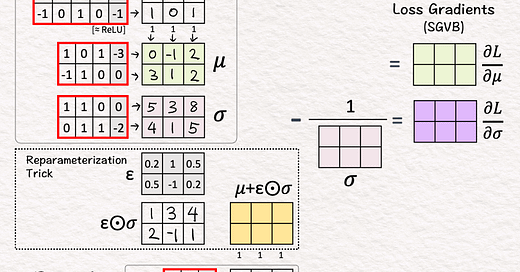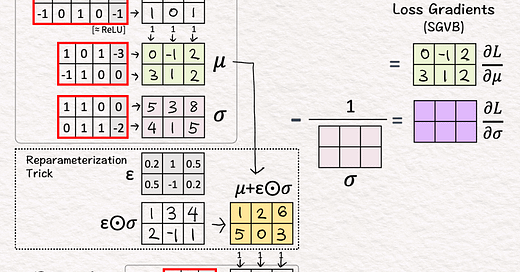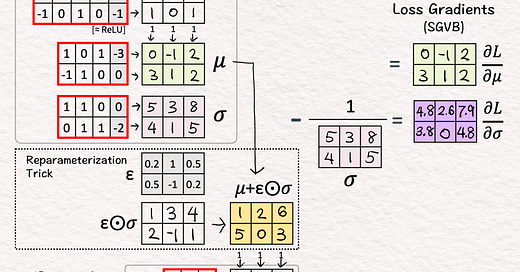
[8]-[10] KL Divergence Loss

[8] Loss Gradient: Mean 𝜇
↳ We want 𝜇 to approach 0.
↳ A lot of math called SGVB simplifies the calculation of loss gradients to simply 𝜇

[9,10] Loss Gradient: Stdev 𝜎
↳ We want 𝜎 to approach 1.
↳ A lot of math simplifies the calculation to 𝜎 - (1/ 𝜎)

[11] Reconstruction Loss
↳ We want the reconstructed data Y (dark 🟧) to be the same as the input data X.
↳ Some math involving Mean Square Error simplifies the calculation to Y - X.