25. Sparse Auto Encoder (SAE)
Can you calculate this by hand? ✍️
Earlier this week, Anthropic published a paper on their latest effort toward interpretable AI:
"Scaling Monosemanticity: Extracting Interpretable Features from Claude 3 Sonnet" by Adly Templeton et al.
The first item in their key results section is:
» Sparse autoencoders produce interpretable features for large models.
How does an SAE achieve interpretability?
Walkthrough
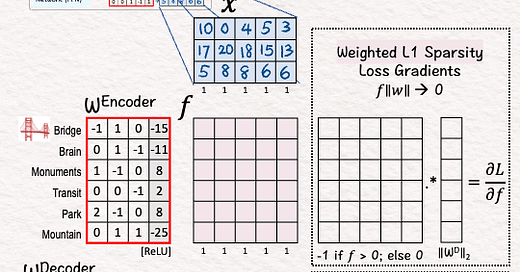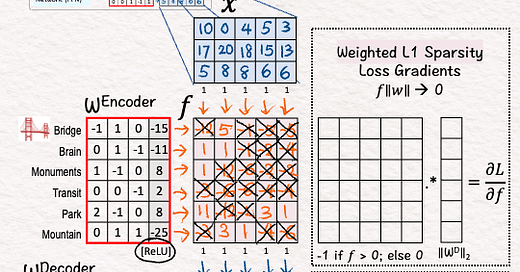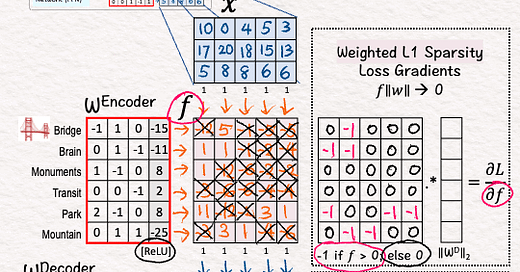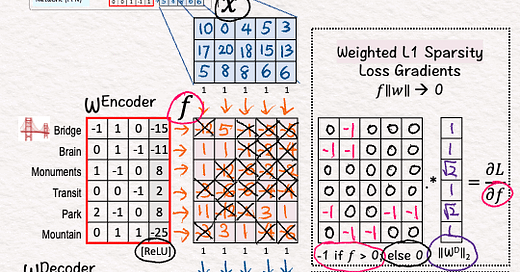
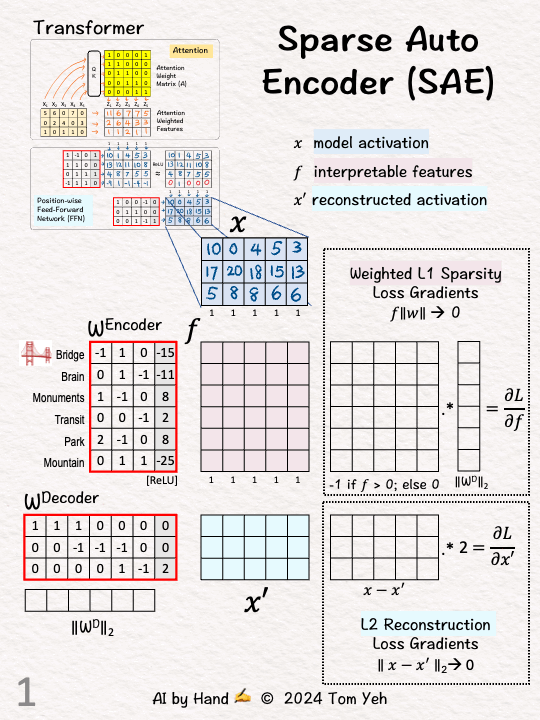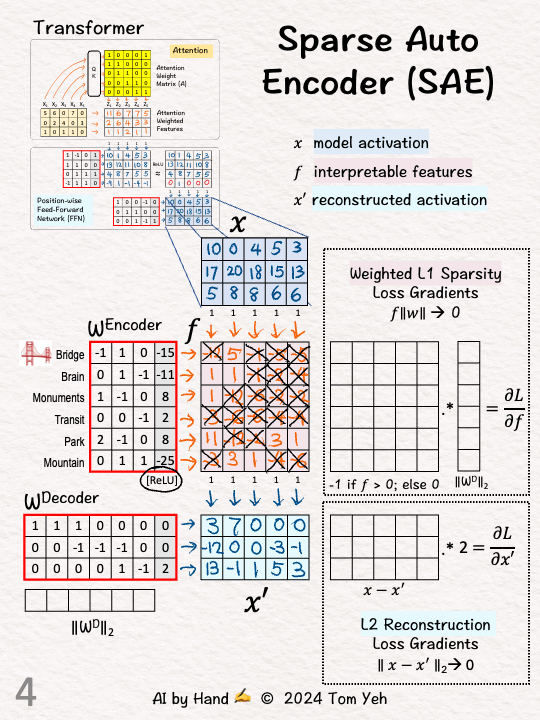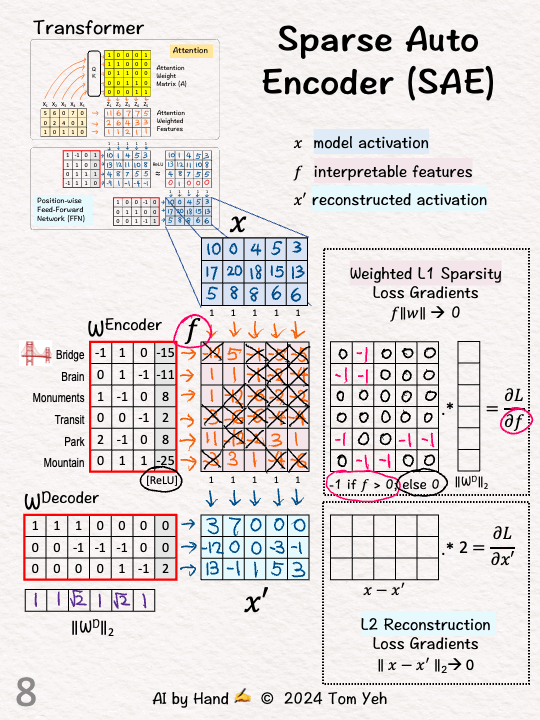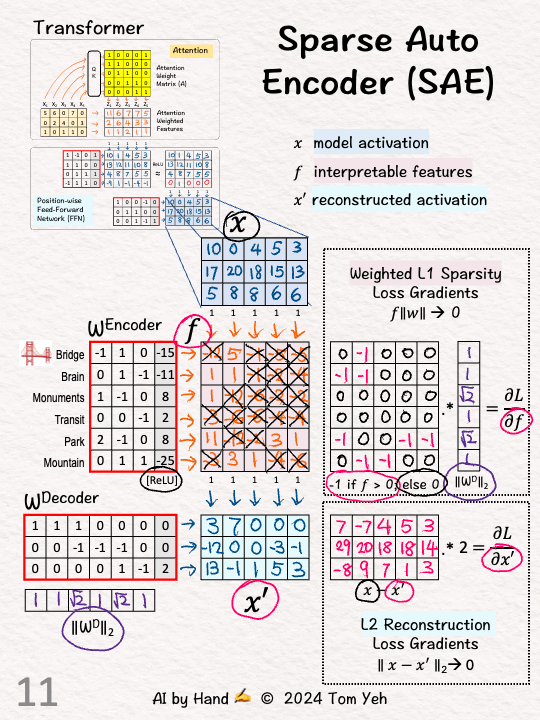
[1] Given
↳ Model activations for five tokens (X)
↳ They work but not interpretable.
↳ Can we map each activation (3D) to a higher dimensional space (6D) that we can interpret?
[2] Encode: Linear Layer
↳ Multiply X with encoder weights and add biases
[3] Encoder: ReLU
↳ Apply ReLU to add non-linearity
↳ ReLU suppresses negative activations (set to 0).
↳ Output: Sparse and interpretable features 𝘧
↳ "Sparsity" means we want many zeros (21/30 here). I hand picked weight and bias values to purposely let ReLU zero out many features.
↳ "Interpretability" is achieved when only one or two features are positive. Here, 𝘟4 and 𝘟5 both have ones only at 𝘧5. By examining the input data, we can guess what 𝘧5 may mean by checking what 𝘟4 an 𝘟5 have in common, for example, both showing a "park."
[4] Decoder: Reconstruction
↳ Multiply f with decoder weights and add biases
↳ Output: X', which is the reconstruction of X from interpretable features.
↳ Reconstruction means we want X' to be as close to X as possible. Here, X' is still quite different from X. More training is needed to update the weights.
[5] Decoder: Weights
↳ Compute L2 norm for each weight column vector. We will use it later
Training 🏋️
[6] Sparsity: L1 Loss
↳ Sparsity means we want as many values in f to zeros as possible. We use L1, which is the sum of the "absolute value" of all the values. We want that sum to be as small as possible.
[7] Sparsity: Gradient
↳ L1's gradient is -1 for positive values, which makes intuitive sense because we want the value to go down to zero.
[8] Sparsity: Zero
↳ For other values that are zero, set gradient values to zero since we don't need to change them.
[9] Sparsity: Weight
↳ Multiply each gradient (row) by the corresponding decoder weight L2 norm.
↳ Goal: To prevent the algorithm from cheating by learning large weight values to reconstruct X.
[10] Reconstruction: MSE Loss
↳ Reconstruction means we want the difference between X and X' to be as small as possible. Here we use L2.
[11] Reconstruction: Gradient
↳ L2's gradient is simply X-X' times 2.
↳ With gradients computed, run backpropagation to update weights for both the Encoder and the Decoder, until we find a good balance between Sparsity and Reconstruction.
