Superposition is a key property that differentiates a qubit in a quantum computer from a bit in a classical computer.
A bit is always in one position.
A qubit can be in many positions simultaneously, until it is measured. This “super” power to be in many positions at once is what enables certain quantum algorithms to achieve exponential speedup!
How can we calculate superposition by hand?
Walkthrough
[1] Given
↳ 3 Qubits: 🟦 a, 🟧 b and 🟪 c.
↳ A quantum circuit with 5 operations involving these 3 qubits.
↳ Because each quantum operation creates two branches, we will show how this circuit is exploring 2 ^ 5 = 32 positions simultaneously.
[2] 🟦 Set a
↳ Qubit a is simultaneously exploring two new branches: |0⟩ and |1⟩
↳ a = |0⟩ means we want a to have a positive chance in |0⟩ and no chance in |1⟩. We write + in |0⟩ and o in |1⟩ to indicate this.
↳ Now, the quantum circuit is exploring 2 positions simultaneously.
[3] 🟧 Set b
↳ Continuing each branch from the previous step, Qubit b is simultaneously exploring two new branches: |0⟩ and |1⟩.
↳ b = |1⟩ means we want b to have no chance in |0⟩ and a positive chance in |1⟩. We write o in |0⟩ and 1 in |1⟩ to indicate this.
↳ Now, the quantum circuit is exploring 2 x 2 = 4 positions simultaneously.
[4] 🟦 H|a⟩ Hadamard Gate
↳ Continuing each branch from the previous step, Qubit a is simultaneously exploring two new branches: |0⟩ and |1⟩ by applying an Hadamard gate.
↳ The main purpose of the H gate is to create “superposition” using the following rules:
+ |0⟩ → + |0⟩ + |1⟩
+ |1⟩ → + |0⟩ - |1⟩
↳ Since a has + in |0⟩, the result is +’s for both |0⟩ and |1⟩.
↳ Intuitively, it is like split the + in the |0⟩ branch into two +’s, one for |0⟩ and one for |1⟩.
↳ Now, the quantum circuit is exploring 2 x 2 x 2 = 8 positions simultaneously.
[5] 🟧 H|b⟩ Hadamard Gate
↳ Continuing each branch from the previous step, Qubit b is simultaneously exploring two new branches: |0⟩ and |1⟩ by applying an Hadamard gate.
↳ Recall the rules are:
+ |0⟩ → + |0⟩ + |1⟩
+ |1⟩ → + |0⟩ - |1⟩
↳ Since b has + in |1⟩, the result is + for |0⟩ and - for |1⟩.
↳ Now, the quantum circuit is exploring 2 x 2 x 2 x 2 = 16 positions simultaneously.
[6] 🟪 Set c
↳ Qubit c is simultaneously exploring two new branches: |0⟩ and |1⟩
↳ c = |0⟩ means we want c to have a positive chance in |0⟩ and no chance in |1⟩. We write + in |0⟩ and o in |1⟩ to indicate this.
↳ Now, the quantum circuit is exploring 2 x 2 x 2 x 2 x 2 = 32 positions simultaneously.
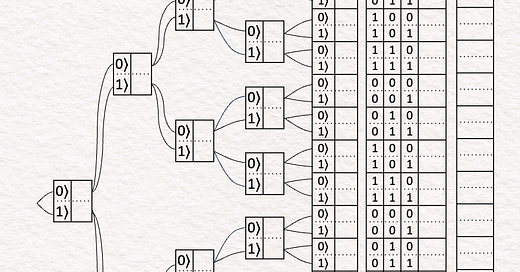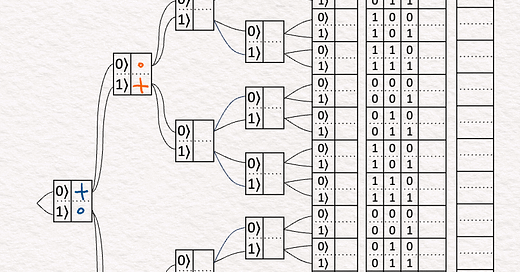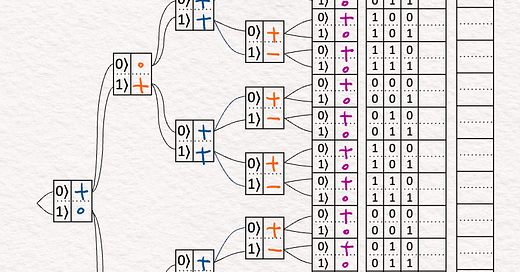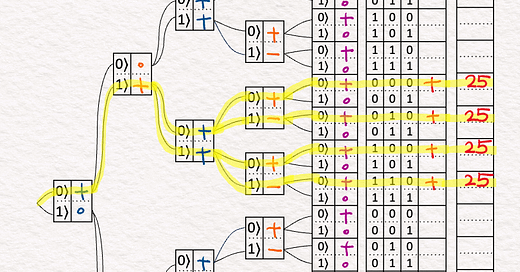
[7] Possible Paths
↳ Even though this quantum circuit is exploring all 32 probable paths simultaneously, only some paths are possible.
↳ If a branch has a 0, it means it is not possible to take the path through the branch.
↳ In other words, if a path has + or - for all the branches along the way, it is possible.
↳ We found only four possible paths without any zero along the way:
000
010
100
110
[8] Quantum Measurement
↳ When taking a measurement, the quantum nature will randomly choose one of the possibilities.
↳ Since there are four possibilities, each possibility has an equal 25% chance of being measured.
↳ Once measured, they collapse into just one of these possibilities.
Discussion
Mathematically, the quantum circuit in this exercise can be calculated using the Dirac notation as follows:
H|0⟩ ⊗ H|1⟩ ⊗ |0⟩
= (1/2) * ( |000⟩ + |010⟩ + |100⟩ + |110⟩)
In developing this exercise, my goal is to invent a simpler and more accessible method to calculate quantum circuits by hand without resorting to difficult math such as Dirac notation, complex numbers, and tensor-product, while yielding the same results.
I would appreciate your feedback. Your feedback will help me develop more exercises like this on other quantum computing topics such as entanglement, control gates, and quantum algorithms like Deutsch–Jozsa, Shor, Bernstein–Vazirani, and Glover.